· しかし同じ次元を持つ量が同じ物理的な意味を持つわけでもないし, わざわざ無理して探すようなものでもない ああ, 動粘度や粘度というものもあったなぁ 粘度の次元は ML1 T1 であり, 単位は Pa・s(パスカル秒) 運動量密度の右隣の空白を埋める3 ニュートンの運動方程式 粒子(または質点、または原子)のニュートンの運動方程式 (3) 上記は、ベクトルを3次元ベクトルとすると3次元モデル 1次元のモデル (4) 1を得る.1次元でのニュートン法と見比べてみると,高次元への自然な拡張となっている ことが分かる.しかし通常は,これを直接扱うのは(逆行列の演算が入っているため)厄 介なので, ∆xi = J 1 xi f(xi) (14) として,これを満たす∆xi を Jx i ∆xi = f(xi) (15)

次元とは何か 改訂版 ニュートンプレス
ニュートン 次元
ニュートン 次元-Pontaポイント使えます! ニュートン式 超図解 最強に面白い!! · 単位の換算 前のページ ;




ダウンロード Newton別冊 超ひも理論と宇宙のすべてを支配する数式 ニュートン別冊 オンライ ン オンラインで読む 無料 ひも理論 科学雑誌 数式
この積層化というプロセス技術に対して、東京応化工業(tok)は、接着剤やキャリア基板といった材料のほか、半導体ウエハのキャリア基板への貼付/分離を行うプロセス機器を開発し、独自のウエハハンドリングシステム(Zero Newton ® )を構築。 このウエハハンドリングシステムは、3次元実装プロセスの大幅な効率化とハイコストパフォーマンスを可能にし次元 ニュートンプレス 発売国日本 書籍 HMV&BOOKS online 支払い方法、配送方法もいろいろ選べ、非常に便利でI超低ずり速度範囲 ニュートン性(第1 ニュートン性領域) Ⅱ中間ずり速度範囲 非ニュートン性の擬塑性 Ⅲ超高ずり速度範囲 ニュートン性(第2 ニュートン性領域) 両対数プロットの粘度曲線*は(b)図のとおりで、Ⅱのずり速
123 1次元1変数方程式に対するNewton法 1 次元1 変数方程式(121) に対する解法を考える。まず,第6 章の平方根の計算で用いたNewton 法の一般形を示す。 アルゴリズム26 (Newton 法(1 次元1 変数方程式)) 1 初期値x0 ∈ R(or C) を設定する。 2 for k = 0,1,2, (a) xk1= xk − f(xk) f′(xk)上式を1次元 マクスウェル 以上述べたように,粘弾性流体の研究はニュートン流体の知見に基づいて発展してきたが,現在は逆に粘弾性流体に関する研究結果が水の流動特性を見直すきっかけを与えている.流体力学におけるBack to the Future対象商品 Newtonライト 次元 (ニュートンムック) ムック ¥935 在庫あり。 この商品は、Amazoncojpが販売および発送します。
Amazonでの次元とは何か―0次元の世界から高次元宇宙まで (ニュートンムック Newton別冊サイエンステキストシリーズ)。アマゾンならポイント還元本が多数。作品ほか、お急ぎ便対象商品は当日お届けも可能。また次元とは何か―0次元の世界から高次元宇宙まで (ニュートンムック Newton別冊この世界が何次元空間かと問われたら,縦・横・高さからなる「3次元空間」と答えるのが普通だと思います。 ところが物理学の最先端では,3次元をこえる「かくれた空間次元」の存在が,真剣に検証されています。 さらにおどろくべき仮説も提唱されています。 現在注目を集めている「ホログラフィー原理」によれば,「3次元空間にみえるこの世界は,実は2次元ここで, 左辺の \( F \) と右辺の垂直抗力 \( N \) はどちらもニュートンという単位( \( \mathrm{N} = \mathrm{kg \cdot m / s^2} \) , 次元は \( \mathrm{MLT^{2}} \) )を持っているので, \( \mu' \) は次元を持っていてはいけない



時間はなぜ1次元 Newton ニュートン ミユウのいろいろ日記




次元のすべて 改訂第2版 ニュートンプレス
2 ニュートンの運動方程式 6 2 ニュートンの運動方程式 21 座標 質点P は直線上を動いているとする。 この点P の座標をx とする。 そして、このx は時刻t によって定 まると考え、次のように表す。 x = f(t) さて、文字を節約して次のように表わすことにする。ニュートン法の収束と発散 • ニュートン法は、曲線の形によっては上手く解 が求まらない場合もある。!31ニュートン重力理論の基本!ニュートンの第一法則=力がかからなければ、 > 等速直線運動を続ける。 !等速直線運動に見える系を「慣性系」と呼ぶ。 " 直線とはどんな空間の直線か?




ヨドバシ Com 次元とは何か 0次元の世界 から 高次元宇宙 まで ニュートンムック Newton別冊サイエンステキストシリーズ ムックその他 通販 全品無料配達




ニュートン別冊の値段と価格推移は 217件の売買情報を集計したニュートン別冊の価格や価値の推移データを公開
0 件のレビュー 990円(税90円) 今、読書のすすめで話題の「次元 」を図解で分かりやすく解説ニュートンの万有引力の式とアインシュタインのエネルギーの式を連立するだけで、 次のことが直ちに分かります: 即ち、Fr=Gm2/r、E=mc2からGm/r=c2にG=Fr2/m2を代入すると、 F=c4/Gとなります。一方、ニュートンの式も成り立っているので、無次元はわかりにくいのでラジアンと呼ぶ 速度 長さ/時間 LT1 m/sec km/h 角速度 角度/時間 sec1 sec1 又は rad/sec rpm 1 分間の回転数 加速度 速度/時間 LT2 m/sec 2 mm/sec 2 力 , 重量 質量×加速度 MLT2 kg ・ m/sec 2 N ニュートン kN




メルカリ ニュートン 次元とは何か 雑誌 800 中古や未使用のフリマ




ヨドバシ Com 次元とは何か 改訂版 0次元の世界から高次元宇宙まで ニュートンムック Newton別冊サイエンステキストシリーズ ムックその他 通販 全品無料配達
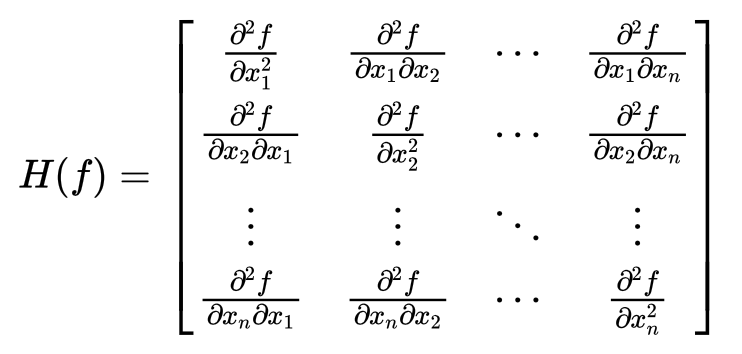
多次元のニュートン・ラフソン法 ニュートン法を連立非線形方程式に一般化する. ベクトル表記では, ここで, である. ステップ目の近似値を とし, の周りで上式をテイラー展開する. ここで, は を の要素とするヤコビ行列である. 2次以上の項10 位置、速度、加速度の関係 11 ニュートンの運動3法則 12 等速直線運動この本は『次元のすべて 改訂第2版 (ニュートン別冊)』の内容を一部抜粋し、イラストや原稿などを大きく加筆・再編集したものです。 そのため「"次元"に関する本を読んで難しくて理解ができない」「まずは"次元"の全体概要だけ理解した」という方に非常におすすめの一冊です。




Jiro Murata




4次元宇宙の謎 時間と空間の最新像にせまる 本 オンライン書店e Hon
· (無次元) 1 立体角 ステラジアン steradian sr (無次元) 1 周波数 ヘルツ hertz Hz s1 力 ニュートン newton N m⋅kg⋅s2 圧力 パスカル pascal Pa N/m2 m1 ⋅kg⋅s2 エネルギー ジュール joule J N⋅m m 2 ⋅kg⋅s2 電力 ワット watt W J/s m 2 ⋅kg⋅s3 電荷 クーロン coulomb C s⋅A 電圧(電位差) ボルト volt V W/A · 発行年月日:12年5月15日 定価:本体2,300円+税 08年4月に刊行したNewton別冊「次元とは何か」は,たいへん好評をいただきました。 このたび,不思議な次元の世界をさらにわかりやすく紹介するため,完成度を高めた"増ページ改訂版"を刊行することとなりました。 私たちは,縦・横・高さでつくられた3次元空間に加え,1次元の時間を合わせた,「4非ニュートン流体モデルを用いた雪崩の3次元非構造有限要素解析 山口 裕矢 , 高瀬 慎介 , 森口 周二 , 寺田 賢二郎 , 小田 憲一 , 上石 勲 著者情報



Kakeru Movie




プリンシピア 自然哲学の数学的原理 第3編 世界体系 アイザック ニュートン 中野 猿人 ブルーバックス 講談社book倶楽部
ニュートン流体の応力による変形 2 次元の粘性流体(ニュートン流体)において,せん断応力や圧力はどのような形で表されるかをみていきま す。流れの中にx,y 座標をとり,それぞれの速度成分をu,v とすると,流体の変形はdu,dv によって生じるこ本書は,1次元の線から,3次元をこえた高次元の空間まで,次元の考え方を楽しく学べる1冊です。 ぜひご一読ください! A5判128ページ,900円+税,9月16日から全国の書店で順次発売 ニュートン式 超図解 最強に面白い!!『次元』のくわしい内容はこちらニュートン別冊 次元のすべて 私たちの世界は何次元なのか? 品切




アイザックニュートンが検疫中に重力を発見



資料詳細
– 接線がx軸と水平になってしまう、つまり接線の傾 きが0 になってしまった場合、発散してしまい解 は求められない。より,ニュートン力学の舞台は,3次元ユークリッド空間と絶対時間(の 直積からなる時空)と考えられる. 参考までに,マイケルソン・モーレーの実験により『あらゆる慣性系 で光の速さ(c)は一定である』ことが確かめられている.この性質(アイ両辺の次元は必ず一致していなければならない。 例えば、ニュートンの運動方程式はF = ma と書かれる。この式は、次元・単位について、左辺の「力」 が質量と加速度の積となることを主張している。力の単位はN(ニュートン)であるから、これは次の関



次元とは何か ちんちらブログ




Newtonライト2 0 次元 ニュートンプレス
ニュートン式 超図解 最強に面白い!! 次元 ツイート;ニュートン法をつかって誤差がどのような振る舞いをするか考える 今, 簡単のために1変数のときを考える 解αが単純孤立した解で, αの近傍でf が 素直な関数でかつ f′(α) ̸= 0 (連立方程式のときは,行列 ∂fi(α) ∂xj が正則)Objective Function ¶ In 0 def func(x1, x2) u = x1 08 v = x2 (a1 a2 * (u**2) * (1u)*(1/2) a3 * u) alpha = b1 b2 * (u**2) * (1u)*(1/2) b3 * u beta = c1 * (v**2) * (1 c2 * v)/(1 c3 * (u**2)) return alpha * npexp(beta) In 0 func(08, 03) Out 0 50




ヨドバシ Com Newton ライト2 0 次元 ムックその他 通販 全品無料配達




ヤフオク 送料無料 3冊 ニュートン別冊 4次元宇宙の謎
一般次元ニュートン力学 目次 x1 質点とその運動 3 x2 エネルギーと仕事 5 x3 場の力と運動方程式 10 x4 保存力と全力学的エネルギー 13 x5 中心力と角運動量 19 x6 座標変換 26 x7 万有引力に従う質点の運動の軌跡の決定(一体問題形) 31 x8ニュートンの単位は、質量に重力加速度をかけたものです。 10kg×98m/s2=98Nで定義されます(10は質量、98は重力加速度)。 中学校の授業では、100g⇒1Nという形で習ったかもしれません。 厳密にいうと100g⇒098Nです。




ダウンロード Newton別冊 超ひも理論と宇宙のすべてを支配する数式 ニュートン別冊 オンライ ン オンラインで読む 無料 ひも理論 科学雑誌 数式



次元のすべて 改訂第2版 ニュートン別冊 Heiman 通販 Yahoo ショッピング




メルカリ ニュートン 次元とは何か 雑誌 800 中古や未使用のフリマ
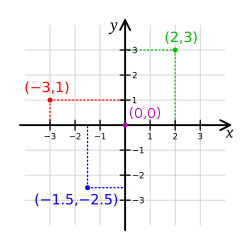



ニュートンの 時間 と 空間 と 座標 の定義 2 デカルト座標 1次元 2次元 3次元 量子力学と意識の変容 宇宙と人間の無限性について




ニュートン式 超図解 最強に面白い 次元 読書のすすめ




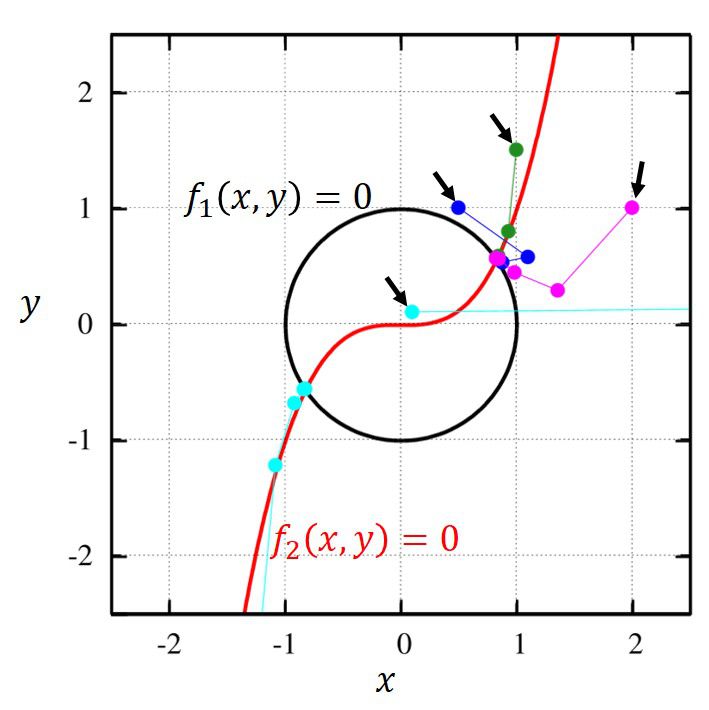
2次元ニュートン法による円と円の交点の数値計算 Qiita
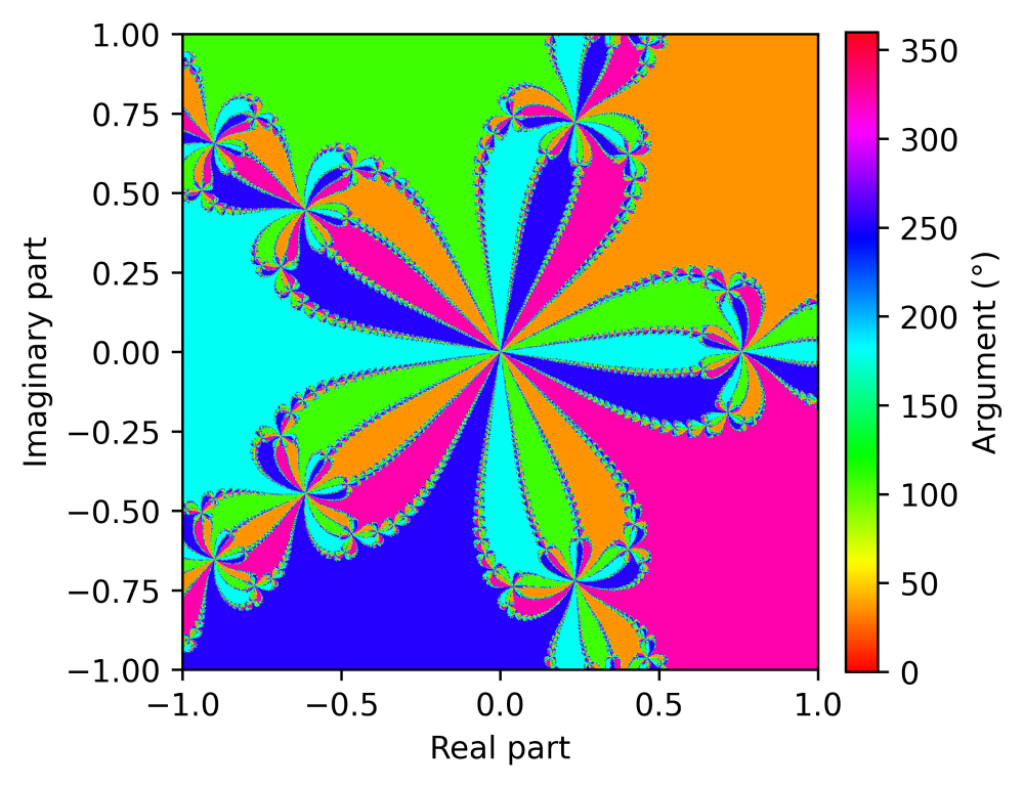



ニュートン法による複素求根アルゴリズム Pythonコード付き Lascode




Suzy 空間を四次元にした場合のニュートン力学で回転系の運動方程式を求めてみると 特段変わったことは起こらず コリオリ力や遠心力や角加速度にかかわる力の項が普通に存在していた




飛行機はなぜ飛べるのか 揚力はなぜ発生するのか その2 ニュートンの空力理論




Newton別冊 次元のすべて ニュートン別冊 本 通販 Amazon




英国王立協会 ニュートンが4次元時空の着想を得ていたことを発表 とね日記



次元 って何 Newton ニュートン ミユウのいろいろ日記




ニュートン別冊 4次元宇宙の謎の値段と価格推移は 5件の売買情報を集計したニュートン別冊 4次元宇宙の謎の価格や価値の推移データを公開




Newton ニュートン 18年3月号 発売日18年01月26日 雑誌 定期購読の予約はfujisan




ニュートン法による複素求根アルゴリズム Pythonコード付き Lascode



ニュートン法 1 2次元 多次元 シキノート




次元とは何か 改訂版 ニュートンプレス




ニュートン単位って何なの ニュートン キログラムに換算してみよう 自分で作ろうインダストリアルな空間を




Newton ニュートン ニュートンプレス 雑誌 定期購読の予約はfujisan



時間はなぜ1次元 Newton ニュートン ミユウのいろいろ日記




ニュートン08年 Daathsan




メルカリ ニュートン 次元とは何か 雑誌 800 中古や未使用のフリマ




ニュートン法 1 2次元 多次元 シキノート




ট ইট র 科学雑誌newton ニュートン 公式 ドラえもんの 四次元ポケット の奥には不思議な 4次元空間 が広がっています 4次元空間とは いったいどんな空間なのでしょうか Newton最新号 18年4月号 の特集 4次元空間を 見る 方法 では 4次元




ニュートン法 Wikipedia



コラム 運動方程式は古典力学の全てだ とある博士が物理の入試問題を解いてみたらこうなった件




ニュートン別冊 4次元宇宙の謎の値段と価格推移は 5件の売買情報を集計したニュートン別冊 4次元宇宙の謎の価格や価値の推移データを公開




ニュートン別冊 4次元宇宙の謎の値段と価格推移は 5件の売買情報を集計したニュートン別冊 4次元宇宙の謎の価格や価値の推移データを公開




2話 ニュートンの蕾 玉響しゆ 少年ジャンプ
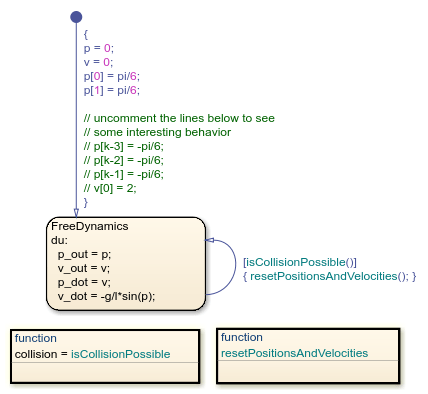



ニュートンのゆりかごのモデル化 Matlab Simulink Mathworks 日本




一言で言えばbfgs 準ニュートン法の紹介




次元のすべて 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア




Newtonライト2 0 次元 ニュートンムック 本 通販 Amazon




Newton別冊 次元のすべて ニュートン別冊 本 通販 Amazon




数学の世界 図形編 ニュートンプレス
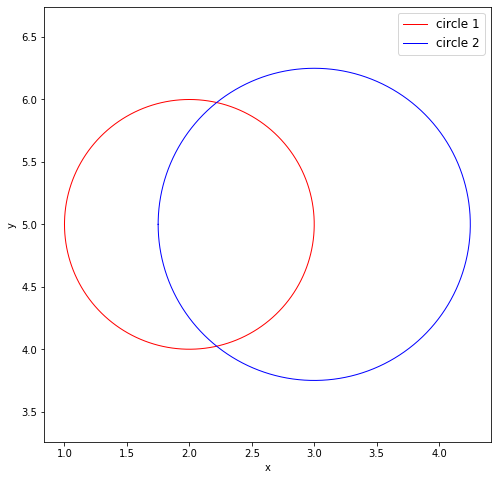



2次元ニュートン法による円と円の交点の数値計算 Qiita




どこにいくのかな キャム ニュートンが行きそうなチーム Nfl超入門 群雄割拠の32国志演義




Newton 別冊 次元の中古 未使用品を探そう メルカリ
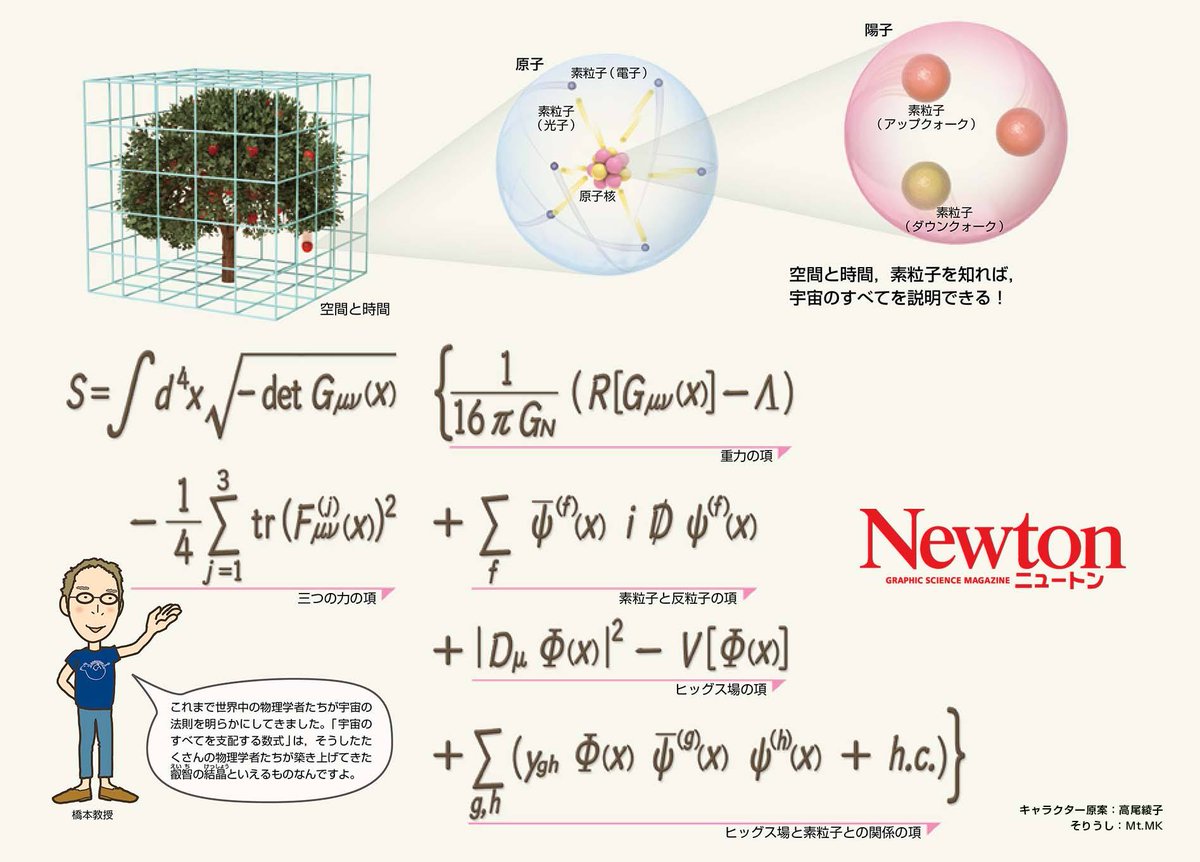



科学雑誌newton ニュートン 公式 Pa Twitter これが 宇宙のすべてを支配する数式 です D X インテグラル ディー 4乗 エックス は その後ろにつづく関数を 宇宙全体 つまり3次元空間と時間のすべてで 足し合わせる 積分する ことを意味します 発売



ニュートンの冥王星とカロンのポスター型カレンダー コンテナ ガーデニング




Newton別冊 次元のすべて ニュートン別冊 本 通販 Amazon




Newton別冊 次元のすべて ニュートンムック Hmv Books Online




綾瀬市にてnewtonなどを買取りしました 神奈川書房




科学雑誌newton ニュートン 公式 超ひも理論の研究をもとに この世界は9次元空間である 空間は幻かもしれない といった驚きの予言もなされています これらはいったい何を意味しているのでしょうか 62ページにわたる特集内で詳しく解説していき




专业雅虎代拍 雅虎拍卖 日本代拍 日拍 日购 Yahoo代拍 转运 代收包裹 日本购物网 Www Gouwujp Com




Newton ニュートン 08 3月号の通販 By Nikko S Shop ラクマ




Newton 別冊 次元の中古 未使用品を探そう メルカリ
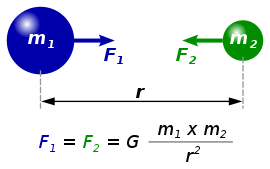



万有引力定数 Wikipedia




ヤフオク ニュートン 雑誌 の落札相場 落札価格




Shiitake S Tumblr Hirai あの方の空手はニュートン力学の域を超え 相対性理論の次元に達しているという




次元とは何か 0次元の世界 から 高次元宇宙 まで ニュートンムック Newton別冊サイエンステキストシリーズ Amazon Com Books




科学雑誌ニュートン 17年11月号 ニュートンプレス



カーボンニュートン フォトビジュアルシリーズ
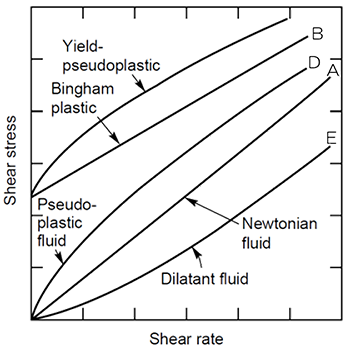



熱流体コラム 非ニュートン流体の1次元解析 Engineering Eye 伊藤忠テクノソリューションズの科学 工学系情報サイト




激ツレェ けど大丈夫 3次元のウサギはいかにして檻から脱出するのか 雨やどりをしよう




ヤフオク Newtonニュートン 自然科学と技術 の中古品 新品 古本一覧




中古 科学雑誌 Newton ニュートン 15 8月から17 11月号まで 28冊 オマケ一冊 物理 生物 化学 医療 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版




理学部の村田次郎教授が科学雑誌 Newton の巻頭特集に登場 立教大学
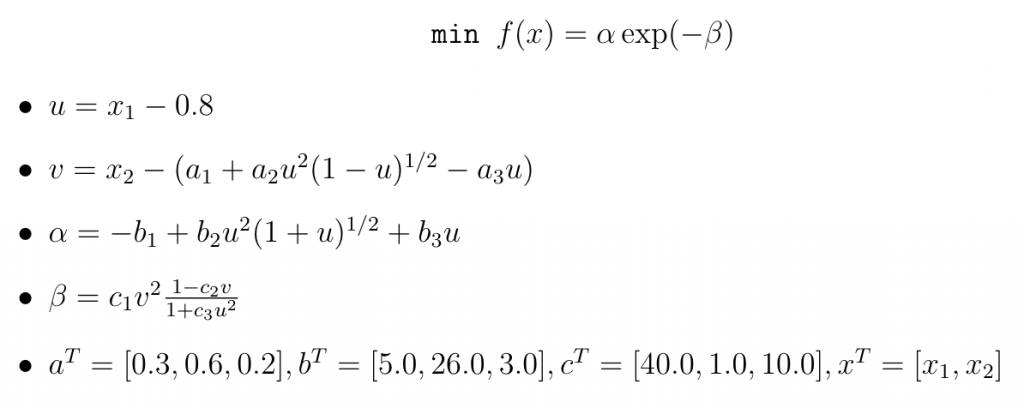



Pythonでやる多次元ニュートン法 Miidas Research



英国王立協会 ニュートンが4次元時空の着想を得ていたことを発表 とね日記




モンスト ニュートンの最新評価 適正神殿とわくわくの実 ゲームウィズ Gamewith




ニュートンとゲーテ 物理学者と文学者が導き出した色の科学 ニュートンとゲーテ 物理学者と文学者が導き出した色の科学 Youtube




ニュートン別冊 4次元宇宙の謎の値段と価格推移は 5件の売買情報を集計したニュートン別冊 4次元宇宙の謎の価格や価値の推移データを公開




Newton別冊 次元のすべて ニュートン別冊




楽天市場 次元 Newtonの通販




18 号 非ニュートン流体とニュートン流体の並行層流を利用したマイクロ粒子分離及び洗浄方法 Astamuse




Newton 別冊 次元のすべて 私たちの世界は何次元なのか 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋




Amazon Co Jp 高次元 Ebook 科学雑誌newton Kindleストア



Kakeru Movie




ニュートン ヨハネの黙示録 の謎を解き明かす鍵が ピラミッドにある と考えていた




次元とは何か 0次元の世界から高次元宇宙まで ニュートンムック Newton別冊サイエンステキストシリーズ 本 通販 Amazon




メルカリ ニュートン 次元とは何か 雑誌 800 中古や未使用のフリマ




ニュートン式 超図解 最強に面白い 次元 ニュートンプレス Hmv Books Online



エクセルを用いたニュートン ラプソン法による非線形方程式の計算




Newtonライト2 0 超ひも理論 ニュートンムック Parapentefamily Com




Newton ニュートン 18年 4月号 Newton編集部 Hmv Books Online



Pythonでやる多次元ニュートン法 Miidas Research




村田次郎 Jiro Murata 別冊newton 次元 のすべて 改訂第2版が届きました 相対性理論から超ひも理論まで 三次元を超える高次元の物理をsfではなく 大真面目に正面から紹介したビジュアルたっぷりの刺激的な一冊になっていると思います 僕の実験も丁寧




読書感想文 ニュートン式超図解 最強に面白い 超ひも理論 からふる Note




高次元の物理学 ニュートン別冊 本 通販 Amazon




Olivia Newton John Come On Over Single Layer Stereo Japanese Import Shm Sacd




ヤフオク 4次元宇宙の謎 改訂版 ニュートンプレス




中身 要約 Newton別冊 虚数がよくわかる 改訂第2版 ニュートン別冊 レビュー Next Topic



0 件のコメント:
コメントを投稿